Packrat Parsing from Scratch

How to implement a packrat parser from scratch, one easy piece at a time.

Estimated reading time: 12 mins

Packrat parsing is a relatively new approach to parsing code introduced by Bryan Ford in his 2002 Master’s thesis. Packrat parsers are capable of very efficiently parsing a class of grammars called Parsing Expression Grammars (PEGs). I covered PEGs in more depth in my previous post, PEGs and the Structure of Languages, so if you’re new to the topic, I recommend you begin there. The packrat parser is based on earlier work on recursive descent parsers, dating back to the 70s, but focused specifically on Parsing Expression Grammars. In this post, I’ll attempt to demystify packrat parsers by walking through a complete packrat parser implementation that fits in a few dozen lines of Javascript code.

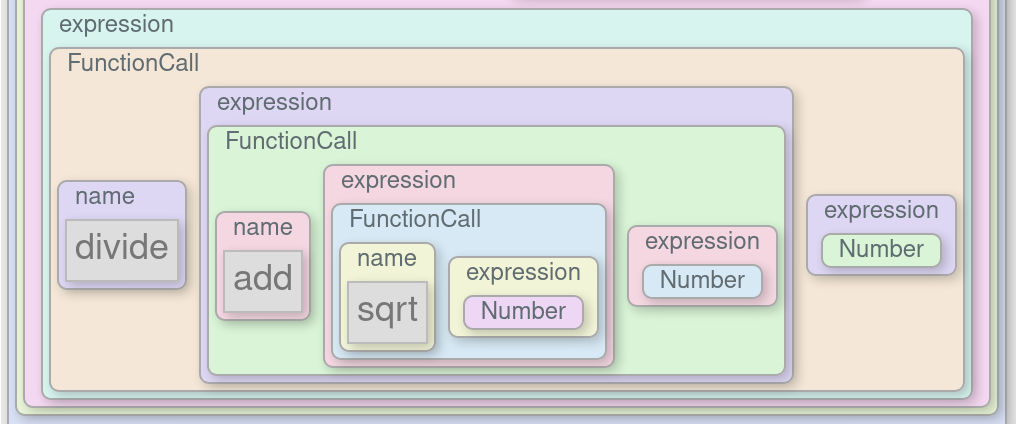
The core idea of the packrat parsing algorithm is incredibly simple. It boils down to: when you attempt to match a rule at a particular position, remember whether it succeeds, and if so, how much input it consumes. Because PEGs have no context-dependencies, if a pattern matches in a particular place in a string, it will always match there, exactly the same, regardless of where it fits into a larger structure. This means there’s a fixed number of combinations of grammar rules to match and string positions to match them at. There’s no need to try matching the same pattern in different ways at the same position. Here, you can see what the parsing algorithm looks like in action (click “Run” to run the demo):

Making a Packrat Parser

The architecture I’m going to use is a functional style that represents grammar rules as functions that will either match an input string or not, and return some information if it does match. This makes the implementation easy, but a more efficient approach might be to use a virtual machine. We’re going to start with a simple container class that stores info about the match:

Here, start is inclusive and end is exclusive, i.e. start is the index where the match begins, and end is the index where subsequent matches would begin. A zero-length match would have start == end.

class Match {
  constructor(text, start, end, children=[]) {
    this.text = text;
    this.start = start;
    this.end = end;
    this.children = children;
  }
}

Pattern Building Blocks

Next, let’s begin implementing support for matching different pattern types. The first and simplest pattern is one that matches literal text. The literal pattern will check whether the exact string match occurs at the starting string position:

In Javascript, functions implicitly return undefined if they run to the end without an explicit return statement, so that will represent “no match.”

function literal(pattern) {
  return ((text, i)=> {
    if (text.startsWith(pattern, i))
      return new Match(text, i, i+pattern.length);
  });
}

Using this, we can perform simple string matching:

var HelloPattern = literal("hello");
HelloPattern("hello world", 0); // -> new Match(text, 0, 5))
HelloPattern("goodbye", 0); // -> no match (undefined)
HelloPattern("hello world", 5); // -> no match at index 5

Great, that works! Let’s get to the meatier patterns. The next pattern is a chain or sequence of other patterns one after the other:

function chain(...patterns) {
  return ((text, i)=> {
    let children = [], start = i;
    for (let pattern of patterns) {
      let result = pattern(text, i);
      if (!result) return;
      children.push(result);
      i = result.end;
    }
    return new Match(text, start, i, children);
  });
}

We can use it like this:

var HelloWorldPattern = chain(
  literal("hello"), literal(" "), literal("world"));
HelloWorldPattern("hello world", 0); // -> new Match(text, 0, 11))
HelloWorldPattern("goodbye", 0); // -> undefined

Now, let’s get to the first really interesting pattern: a branching choice option. This will walk through a list of patterns one at a time, and return the results of the first one that succeeds:

function oneof(...patterns) {
  return ((text, i)=> {
    for (let pattern of patterns) {
      let result = pattern(text, i);
      if (result) return result;
    }
  });
}

We can use it like this:

var AddressWorldPattern = chain(
  oneof(literal("hello"), literal("goodbye")),
  literal(" "), literal("world"));
AddressWorldPattern("hello world", 0); // -> new Match(text, 0, 11))
AddressWorldPattern("goodbye world", 0); // -> new Match(text, 0, 13)
AddressWorldPattern("hello sky", 0); // -> undefined

At this point, we need a way to match repeating patterns. There’s two ways to do that: looping and recursion. I’m going to choose recursion here because it will make it easier to have a fine-grained cache in the future (this will have one recursive function call per iteration). The approach for recursion is to recursively define “0 or more repetitions of a pattern” to mean: either the pattern followed by 0 or more repetitions of the pattern, or the empty string (in PEG syntax: repeating <- (pat repeating) / ""). Because PEGs formally specify parsing order, the empty string will only match if “one or more repetitions” doesn’t match:

The code here uses a lazy lookup of zero_or_more using a function closure. This is a little hacky, but later, we will implement a less hacky way to do this.

function repeat(pattern) {
  let zero_or_more = oneof(
      chain(pattern, (text,i)=>zero_or_more(text,i)),
      literal(""));
  return zero_or_more
}

These four primitive pattern types (literals, chains, options, and repeating) are incredibly powerful, and you can define a huge range of PEG grammars in with only these tools, but there’s one thing missing: negation. Negation will allow us to specify that something shouldn’t match a pattern (e.g. variables can’t be keywords). A successful negation will return a zero-length result that means “the pattern I’m negating doesn’t match at my starting position:”

function not(pattern) {
  return ((text, i) => {
    if (!pattern(text, i))
      return new Match(text,i,i);
  });
}

Now, the last component here isn’t strictly necessary, but it’s very handy to have a wildcard pattern that matches any single character, the equivalent of . in regular expressions. You could achieve the same goal by creating a oneof() that has a literal() corresponding to every character, but that’s just tedious.

function anychar() {
  return ((text, i)=> {
    if (i < text.length)
      return new Match(text, i, i+1);
  });
}

A Simple CSV Parser

With these functions, we can implement a parser for a full language! Let’s try it out with a CSV parser (comma separated values) to see what it will look like:

// Equivalent to the regex: [^,\n]*
let CSVItem = repeat(chain(not(","), not("\n"), anychar()));
// Sorta like: CSVItem ("," CSVItem)*
let CSVLine = chain(CSVItem, repeat(chain(",", CSVItem)));
// Sorta like: CSVLine ("\n" CSVLine)*
let CSVFile = chain(CSVLine, repeat(chain("\n", CSVLine)));

// It works (but only for validation)
let my_file = "x,y,z\na,b,c";
Console.assert(CSVFile(my_file)) // new Match(...)

Capturing Data

Right now, the parsing framework is very flexible, but it’s not very useful because the return value it produces is just a bunch of string indices. Let’s add the ability to explicitly capture snippets of the source text and the ability to tag a match with a descriptive name.

function capture(pattern) {
  return (text, i)=> {
    let result = pattern(text, i);
    if (result) {
      let match = new Match(
        text, result.start, result.end, [result]);
      match.captured = text.substring(i, result.end);
      return match;
    }
  };
}

function named(name, pattern) {
  return (text, i)=> {
    let result = pattern(text, i);
    if (result) {
      let match = new Match(text, i, result.end, [result]);
      match.name = name;
      return match;
    }
  };
}

Now we can define our earlier grammar with captures:

let CSVItem = named("Item",
  capture(repeat(chain(not(literal(','),
    not(literal("\n")), anychar()))));
let CSVLine = named("Line",
  chain(CSVItem, repeat(chain(literal(','), CSVItem))))
let CSVFile = named("File",
  chain(CSVLine, repeat(chain(literal("\n"), CSVLine))))

This finally gets us to a usable result! Here’s a program that uses our CSV parser to print the sum of the numbers on each row.

let my_file = "1,2,3\n4,5,6"
let csv_data = CSVFile(my_file):

// Extract the captured values from the tree structure
// of chain()s and oneof()s and so forth:
function* get_captures(n) {
  if (n.captured) yield n.captured;
  for (let child of n.children) {
    yield from get_captures(child);
  }
}

// Print the sum of the numbers on each row:
for (let row of csv_data.children) {
  let total = 0;
  for (let item_text of get_captures(row)) {
    total += parseInt(item_text);
  }
  console.log(total); // First logs 6, then 15
}

Recursion

Earlier, when we defined the repeat rule, we had to use a somewhat hacky version of recursion that relied on local variables and function closures. It worked, but it wasn’t clean. The way to solve this more elegantly is to use lazy rule lookups on a single grammar object:

class Grammar {
  ref(name) {
    return (text, i) => this[name](text, i);
  }
}

Using this object, we can implement recursive (and corecursive) definitions by using grammar.ref() instead of referencing the rule directly, and the lookup will be delayed until after the rule is defined:

let g = new Grammar();
g.A = chain("A", oneof(g.ref("A"), g.ref("B"), literal("")));
g.B = chain("B", oneof(g.ref("B"), g.ref("A"), literal("")));
g.AB = oneof(g.A, g.B);
Console.assert(g.AB("ABBBAAABA", 0));

Some Conveniences

There’s also a few other helper functions that provide some features you might expect or desire to have, like lookaheads (&patt), optionals (patt?), character ranges ([a-z]), character sets ([aeiou]), and inverted character sets ([^,;]). All of these can be implemented in terms of the previously defined functions, but they’re common enough that it makes sense to make slightly more optimized versions of them and provide an API to access them easily.

// Equivalent to not(not(pattern))
function ahead(pattern) {
  return (text,i)=> (pattern(text, i) && new Match(text, i,i));
}

// Equivalent to oneof(pattern, literal(""))
function maybe(pattern) {
  return (text,i)=> (pattern(text, i) || new Match(text, i,i));
}

// Equivalent to oneof(literal(min), ..., literal(max))
function between(min, max) {
  return ((text, i)=> {
    if (i < text.length && min <= text[i] && text[i] <= max)
      return new Match(text, i, i+1);
  });
}

// Equivalent to oneof(literal(allowed[0], allowed[1], ...))
// or chain(not(oneof(...)), anychar()) when inclusive=false
function charfrom(allowed, inclusive=true) {
  if (!inclusive)
    return chain(not(charfrom(allowed)), anychar());
  return oneof(...allowed);
}

All right! That’s it. In total, it’s about 100 lines of code for a full parsing library that can parse any arbitrary PEG. Unfortunately, it’s kinda slow because it’s not a proper packrat parser. The defining feature of packrat parsers is that they memoize everything, which is what gives them their amazing speed.

Packrat Parsing

We can make this code orders of magnitude faster with 10 lines of code, and one tiny tweak. All it takes adding caching to the definitions:

function cached(fn) {
  let cache = {}, cache_text = "";
  return (text, i)=> {
    if (text != cache_text) // cache is per-input-text
      cache = {}, cache_text = text;
    if (!(i in cache))
      cache[i] = fn(text, i);
    return cache[i];
  }
}

And then, wrap all the returned functions with cached(). For example, with literal():

function literal(pattern) {
  return cached((text, i)=> {
    if (text.startsWith(pattern, i))
      return new Match(text, i, i+pattern.length);
  });
}

That’s it! This is a complete packrat parser! As you’ve seen, the fundamental components of a packrat parser are individually quite simple, and there aren’t very many of them. At its heart, a packrat parser is nothing more than a memoized matcher of literals, chains, choices, negations, and recursive references. There’s nothing that’s fundamentally difficult to understand, just a simple idea that can be implemented in a few dozen lines of code and endlessly tweaked and improved on.

Future Improvements

The parser that I’ve walked you through implementing in this post is asymptotically quite fast. It runs in $O(G N)$ time, where $G$ is the size of the grammar and $N$ is the size of input text; in other words, for a fixed grammar, you will get $θ(N)$ performance for arbitrary input text. It will also use $O(G N)$ memory space ($θ(N)$ for a fixed grammar). For comparison, packrat parsers are capable of matching recursive grammars that are impossible to match with extended regular expressions, but can do so in linear time, while extended regular expressions have potentially unbounded runtime. The downside is that packrat parsers use an amount of memory proportional to the length of the input text. Packrat parser runtime may be close to $θ(N)$ for arbitrary real-world (non-malicious) grammars, since grammars tend to follow power-law distributions, where a few rules are called often, but the rest are only rarely called. When this is the case, the expected number of rules tested at each string index is bounded by a constant number that doesn’t grow as the grammar adds more rules. However, the implementation here has a lot of constant-time overhead on common operations and it can potentially use quite a lot of stack space. Using a virtual machine with a heap-allocated stack instead of recursive function calls will lower function call overhead and prevent stack overflow, but the overall performance would need to be tuned using a profiler to find performance bottlenecks if you truly cared about speed. In other words, this blog post is intended to give you an understanding of the concepts behind a packrat parser, but the code here won’t outperform a real parsing library.

Besides performance, the programming ergonomics could also use a lot of improvement. The code repeat(charfrom('aeiou'))(input_text, 0) is much more cumbersome than regex pattern matching: input_text.match(/[aeiou]*/). Fortunately, the regex/BNF-like PEG grammar discussed in PEGs and the structure of languages is itself a grammar that can be parsed by a packrat parser. In my next post, I’ll discuss how to write a program that automatically converts PEG-syntax grammars into runnable parsers–in other words, how to make a parser-generator. As a quick teaser, here is how we might start building it:

let g = new Grammar();
g.AnyChar = named("AnyChar", literal("."));
g.CharSet = named("CharSet", chain(literal("["),
  repeat(not(literal("]")), capture(anychar())),
  literal("]")));
// ...
g.Expression = oneof(
  g.ref("AnyChar"), g.ref("CharSet"), ...);

function make_parser(grammar_text) {
  let match = g.Expression(grammar_text, 0);
  if (!match) throw "Grammar failed to compile";
  switch (match.name) {
    case "AnyChar": return anychar();
    case "CharSet": return charfrom(get_captures(match));
    //...
  }
}
function match(grammar, text, offset=0) {
  return make_parser(grammar)(text, offset)
}

let result = match("[aeiou]", input_text);

Look forward to a new post coming soon!